LO QUE ENCONTRAREMOS EN ESTE SITIO NO SUSTITUYEN LAS CLASES, SOLO SON MATERIALES QUE PUEDEN ENRIQUECERLAS Y COMO AYUDA PARA RESOLVER DUDAS.
FORMAS SIMPLES
QUÉ ENTENDEMOS POR SIMPLICIDAD?
En primer lugar, podemos decir que es la experiencia y el juicio subjetivos de un observador que no halla dificultad para entender aquello que se le presenta. Cuando las cosas están dispuestas de tal modo que al sernos representadas por los sentidos podemos imaginarlas fácilmente y, en consecuencia, recordarlas fácilmente, decimos que están bien ordenadas, y en caso contrario, mal ordenadas o confusas. Se determina, pues , la simplicidad de los objetos visuales, analizando sus propiedades formales.
LA LÍNEA RECTA
Línea recta es simple porque utiliza una sola dirección invariable. Las líneas paralelas son más simples que las que forman ángulos porque su relación está definida por una distancia constante. Un ángulo recto es más simple que otros porque produce una subdivisión del espacio basada en la repetición de un mismo ángulo.
Aquí encontramos un ejemplo de trazos paralelos
Encontramos allí diferentes rectas, un horizontal, una vertical, una oblicua.
Debajo encontramos rectas paralelas y otras perpendiculares, o sea que cuando se cortan forman un ángulo de 90 grados.
Esas son las diferentes rectas que podemos encontrar en una composición, pero luego nos van a ayudar a entender mejor los conceptos de proyecciones y de perspectiva.
Las rectas paralelas nunca se cortan, tiene la misma distancia entre sí, porque las rectas están conformadas por un conjunto de puntos alineados, cada punto de una de esas rectas mantiene la misma distancia que el punto de la otra recta. La otra condición de las rectas paralelas es que deben pertenecer al mismo plano. Si imaginas el pizarrón, las dos rectas paralelas tienen como mismo plano el propio pizarrón.
En cambio en las rectas perpendiculares siempre cuando se cortan lo hacen a 90 grados, formando lo que se llama un ángulo recto.
LA PRIMERA PROPUESTA CONSISTE EN: ELABORAR UNA COMPOSICIÓN DONDE ENCONTREMOS LÍNEAS PARALELAS, GENERANDO ESPACIOS, QUE LUEGO RELLENAMOS CON TRAZOS. Puede ir acompañada de puntos también como se ve en el ejemplo.
Les mando ejemplos de cómo podemos hacer la composición, la cual puede ser a mano alzada o con instrumentos.
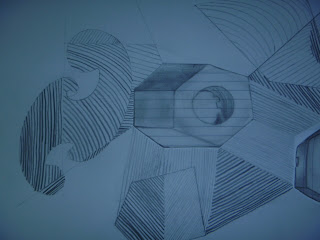
Estos ejemplos son de compañeros que resolvieron el ejercicio de esta manera, ésto les pude ayudar a tener una idea de como resolverlo. Ellos integraron piezas mecánicas y luego rellenaron el espacio con trazos.
RECONOCEMOS VOLUMENES
Los contornos primarios pueden dilatarse o girar hasta generar formas o sólidos volumétricos distintos, regulares y fácilmente reconocibles. Las circunferencias generan esferas y cilindros, los triángulos generan conos y pirámides y los cuadrados generan cubos. Aquí, el término sólido no se refiere a la consistencia de la materia, sino a los cuerpos o figuras geométricas tridimensionales.
Tridimensionales significan que tienen, largo, ancho y altura.
En este ejemplo puedes ver, una esfera, un cubo, un tetraedro (pirámide de base triangular, que tiene 4 lados y son todos iguales entre sí, y que a su vez son triángulos equiláteros).
Mas abajo tenemos un cilindro y un cono. Estos últimos llamados volumenes de revolución porque tiene un eje imaginario en el centro, por donde los mismos giran, esto los veremos más adelante.
LOS LÍNEAS SON CONJUNTO DE PUNTOS ALINEADOS, PERO SE ENCUENTRAN EN UN SOLO PLANO.
LOS VOLUMENES SON DIFERENTES, TIENES QUE IMAGINAR EL SALÓN DE CLASE RELLENO DE GRANOS DE ARENA. SON INCONTABLES, INFINITOS. LO MISMO SUCEDE CON CUALQUIER VOLUMEN, ESTÁN RELLENOS DE PUNTOS IMAGINARIOS, AL IGUAL QUE LA ARENA DEL MAR, POR LO TANTO NO ESTÁN EN UN SOLO PLANO, ESTÁN DENTRO DE UN VOLUMEN. ACÁ LOS PUNTO IMAGINARIOS SON PARA RELLENAR UN VOLUMEN Y NO ESTÁN EN UN SOLO PLANO, ES TODO EL ESPACIO CON LOS MISMOS.
En este caso tenemos un fotografía de la ciudad de Brasilia, capital de Brasil.
Como podemos ver, esta ciudad al igual que muchas otras es un conjunto de volumenes, que en realidad también tienen que ver con lo los volumenes que hablamos anteriormente, ahí podemos ver, prismas, que en la realidad son los edificios, las calles podríamos decir que son figuras rellenas, son rectángulos rellenos. Las ventanas tienen detalles arquitectónicos que consisten en vigas o pilares que forman una malla de rectas paralelas y perpendiculares.
Las piezas mecánicas también cuando las representamos encontramos líneas paralelas y líneas perpendiculares, sabemos que las piezas son volumenes, pero para dibujarlas solo lo podemos hacer en una hoja, representando las mismas solo en forma plana. Las formas tridimensionales pasan a un formato que le llamamos bidimensional, o sea, ancho por largo.
Ahí vemos un engranaje pero solo lo podemos ver de frente, para dibujar el mismo tendremos que diagramar diferentes círculos, las otras piezas que son cilíndricas las representamos como si fueran rectángulos
EL SEGUNDO EJERCICIO CONSISTE EN UNA COMPOSICIÓN DONDE ENCONTREMOS ESPACIOS RELLENOS Y OTROS NO RELLENOS, COMO VEMOS EN LA FIGURA ANTERIOR, no tienen por qué tener una pieza mecánica, pueden tener figuras geométricas.
UNOS ESPACIOS QUEDARÍAN TODOS RELLENOS PINTADOS, OTROS CON TRAZOS Y OTROS NEUTROS, O SEA SIN RELLENAR.
En esta composición del artista Pablo Picasso, encontramos espacios neutros, espacios rellenos y espacios con trazos. (como para darles una idea de como debe quedar el trabajo).
FORMAS SIMÉTRICAS Y FORMAS ASIMÉTRICAS
Esta composición tiene por título:"blow up", del artista indonesio YUDI YUDUYOKO.
Corresponde a un ejemplo de simetría axial.
Si miras esta composición, podemos notar en ella que si trazamos una recta exactamente en la mitad de la misma, los dibujos que la componen se repiten pero en forma inversa. Es como si dobláramos la hoja en la mitad e hiciéramos coincidir los dibujos de un lado y del otro.
Este otro ejemplo es de simetría radial o central.
LA SIMETRÍA DE UNA FORMA SE PERCIBE POR LA PRESENCIA DE PARTES DE DICHA FORMA QUE SE PUEDEN SUPERPONER
Todos estos ejemplos corresponde a simetría radial
SIMEORTRÍA CENTRAL, SON FORMAS CUYOS ELEMEMENTOS SE ENCUENTRAN EQUIDISTANTES DE UN PUNTO (CENTRO DE SIMETRÍA).
SIMETRÍA AXIAL ES CUANDO LAS FORMAS SE ENCUENTRAN EQUIDISTANTES DE UNA RECTA O EJE DE SIMETRÍA.
*
*
Si trazáramos un eje exactamente en la mitad de esta imagen (donde encontramos los asteriscos), el diagrama o dibujo coincide exactamente de un lado que en el otro. En otras palabras, el eje se encuentra en el medio del dibujo, las otras rectas o los cuadrados tiene exactamente la misma distancia de un lado que del otro del eje de simetría.
*
*
Acá tenemos otro ejemplo de simetría axial, si trazamos un eje que cruce el dibujo, las dos partes son iguales y opuestas entre sí.
*
*
Otro ejemplo de simetría axial, lo mismo se repite de un lado y del otro, manteniendo de los dos lados las mismas distnacias del eje de simetría.
TERCERA PROPUESTA
DIAGRAMAR UNA COMPOSICIÓN DONDE ENCONTREMOS SIMETRÍA AXIAL.
PUEDES USAR FIGURAS GEOMÉTRICAS O ALGUNA PIEZA MECÁNICA QUE PUEDAS TENER EN CASA, YA QUE LA MAYORÍA DE LAS PIEZAS TIENEN SIMETRÍA
Puedes usar colores para pintar la misma, basándote en los ejemplos no creo pueda ser difícil, pero igualmente voy a enviar otro ejemplo para que lo puedas analizar mejor.
MUCHA SUERTE,....ESPERO SUS TRABAJOS.
POR EL MOMENTO SON TRES PROPUESTAS
A) COMPOSICIÓN SOLO CON TRAZOS.
B) COMPOSICIÓN CON ESPACIOS NEUTROS, RELLENOS Y TRAZOS.
C) COMPOSICIÓN CON SIMETRÍA AXIAL.
